
幾何公差って何?
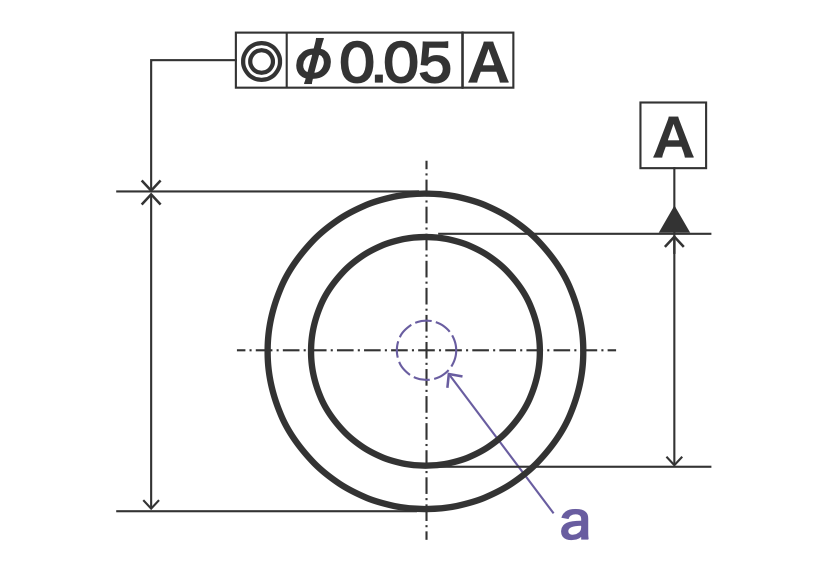

図面にこのような記号が記載されているのを見たことがありますか?
こういった記号で示されているのが幾何公差です。
記号によって様々な意味があり、画像のものは左から同心度、直角度、平行度を表しています。
例えば同心度0.05であれば、図の2円の中心のズレが0.05mm以内で作れという指示です。
15もの種類がある幾何公差ですが、本記事では切削加工を行っていくにおいてよく目にするものを紹介します!
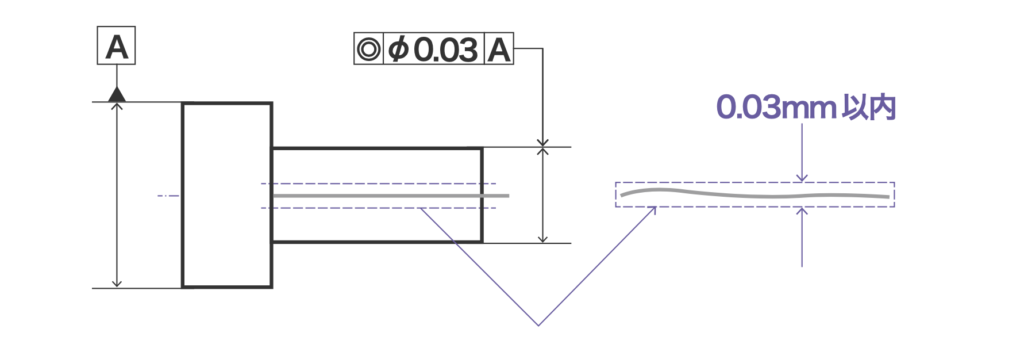
真直度
丸ものの真直度
直線形体の幾何学的直線からの狂いの大きさ
機械製図 実教出版
主にシャフトの曲がり具合を指定しているのがこの真直度です。
長尺物なんかに入っていることがありますが、削りがあると残留応力でどうしても曲がってしまうため厄介な公差です。
このようにシャフトの径寸法を指示する線に真直度の公差が入っているような場合でも、図のように「シャフトの中心線が0.1mm以上ズレてはいけない」という意味になります。
板ものの真直度
真直度は、平面ではなく直線に対する公差です。
なので板ものの場合でも丸ものと同じように、中心線が公差内に入っているかどうかを指示しています。
丸ものの真直度の測定方法
このような公差が入っている場合は、曲がり具合を測定してやれば良いです。
例えばシャフトの場合、旋盤で比較的端の方を掴んで2点芯出しを行った上で、シャフトを回して最も振れている箇所の振れをダイヤルゲージで測定することで真直度を測れます。
三つ爪チャックを使っている場合などで2点芯出しが難しい場合は、シャフトの両端をVブロックで受け、Vブロックで受けたところの高さをぴったり合わせた上でシャフトを回します。
最も振れている箇所の振れを読み取ればそれが真直度です。
いずれの方法もシャフトの自重で曲がってしまうと正確な真直度が測定できないので注意しましょう!
板ものの真直度測定方法
板物で真直度が入っている場合はなかなかありませんが、一応測定方法を説明しておきます。
まずはシャフトのVブロックの方法と同じように板の両端を支えて支えた箇所の高さを合わせます。
そしてダイヤルゲージを板の中心を通るようにスライドさせて最大値と最小値の差を読み取ればそれが真直度です。
ちなみにダイヤルゲージを中心に走らせる理由は、端の方を走らせると板がねじれている場合に正確に真直度を測れないためです。
平面度
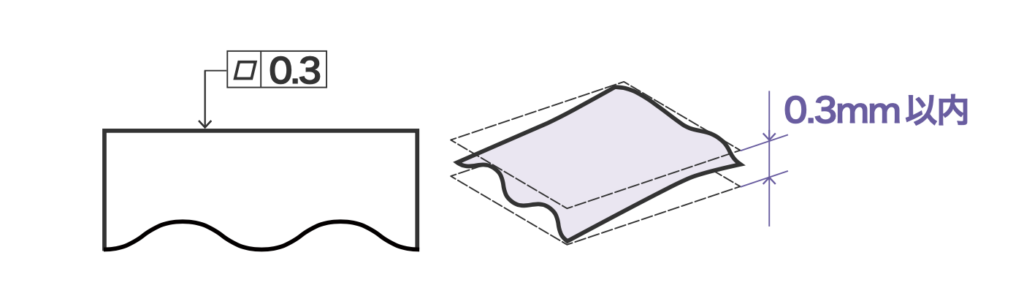
平面形体の幾何学的平面からの狂いの大きさ
機械製図 実教出版
平面度は、図のように平面がどのくらい平らであれば許されるかということを指示したものです。
指示されている平面が、0.3mm離れた平行な平面の間になければならないということですね。
平面なんて平らで当たり前だろうと思いがちですが、例えばフライス加工を行って平面が歪んでしまうことがよくあり、その歪み具合によっては平面度公差はなかなか厄介な公差になり得るんです。
旋盤では平面度公差はほとんど出会うことはありませんが、特にアルミなんかは残留応力で端面が反ってしまうことがあるので、もし平面度公差が入っていたら気をつけて加工したほうが良いです。
平面度の測定方法
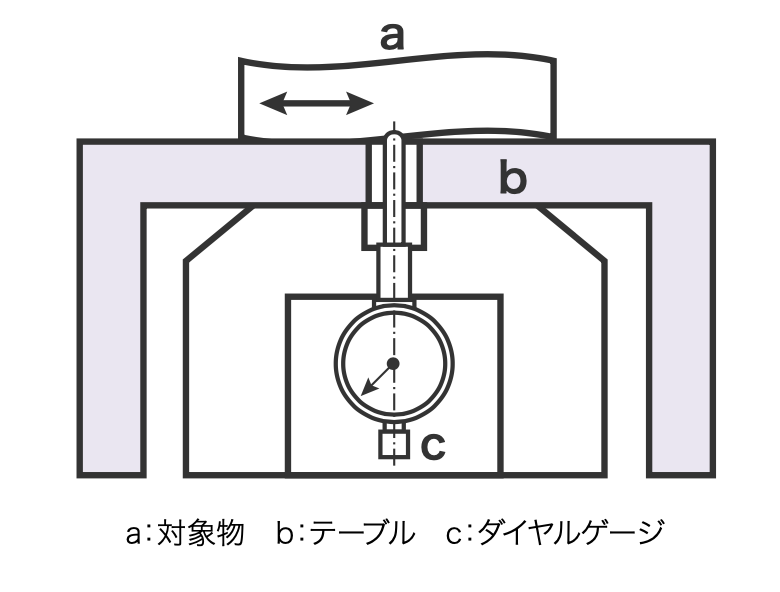
平面度の測定はなかなか厄介です。
きちんと測定しようと思うと、図のような治具を作ってワークを動かし平面度を測定する必要があります。
平面のうちの最大値と最小値の差が平面度です。
ハイトゲージにダイヤルゲージを取り付けての測定方法だと接地面の傾きに影響されてしまうため、図のような治具を使わなければ正確には測定できません。
勤務先で実際に測定する場合は、キーエンスの簡易三次元測定機を使います^^;
真円度

円形形体の幾何学的円からの狂いの大きさ
機械製図 実教出版
丸ものにおいて、楕円などではなく範囲内の真円になっているかどうかを指定した公差です。
画像のように、真円度0.1であれば0.1mm離れた2つの円の間にあればOKです。
主に薄物に入っている公差で、旋盤で加工する場合はチャック圧や残留応力によってひずみがでないように加工する必要があります。
旋盤でも薄物のリングは真円度が狂いやすく、真円度が入っているとなかなか厄介で工夫して加工しなければ歪んでしまいます。
加工方法のコツはこちらの記事にまとめていますので参照してください!
真円度の測定方法
真円度の測定はダイヤルゲージを使って2点間を測定する方法もありますが、手締めのスクロールチャックを装備した旋盤を使って測定するのが簡単です。
まずはワークを潰さないように、なるべく測定箇所に影響がない部分をそ〜っとつかみます。
それから芯出しを行い、その上でワークを回転させてダイヤルゲージで最大値と最小値を読み取ります。
そして、その最大値と最小値の差の二分の一が真円度になります。
平行度

データム直線またはデータム平面に対して平行な幾何学的直線または幾何学的平面からの平行であるべき直線形体または平面形体の狂いの大きさ
機械製図 実教出版
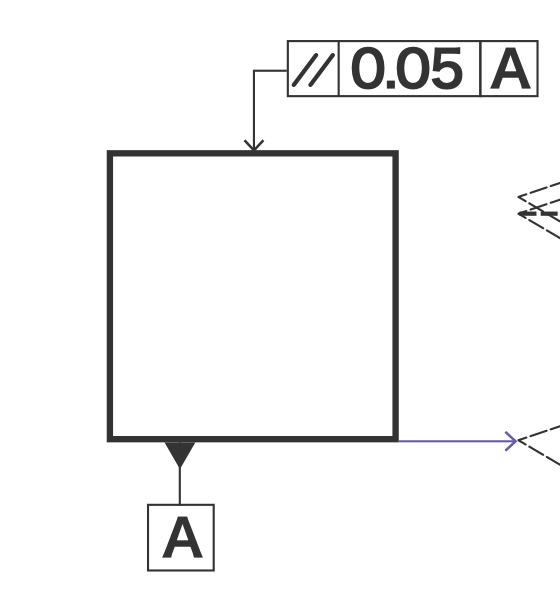
平行度は、データムという指示線で示された平面に対して、平行な平面であることを示した公差です。
平面だけでなく直線にも適用される幾何公差ですが、現場の図面では平面に対して見ることが多いです。
旋盤加工では、フランジの端面同士に入っていることが多い公差です。
NC旋盤であればきちんと端面の芯が出ている爪を使って加工すれば大概は問題ありませんし、後述しますが測定も簡単です。
データムとは?
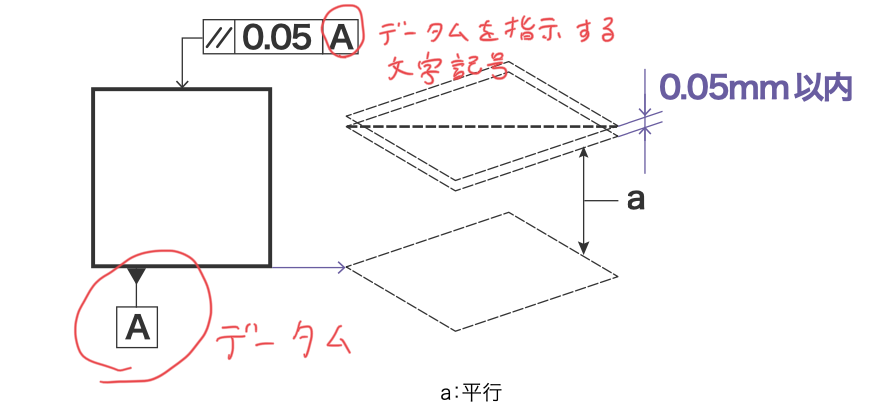
本項の平行度からデータムを使った幾何公差になりますので、このタイミングでデータムについて解説しておきます。
データムというのは画像のように、平面や直線を示す文字記号です。
例えば上の図面だと、データムAで示された平面に対して0.05mm以内の平行度が求められているという意味になります。
つまり平行度の理解としては、図のようにデータムAに平行な、0.05mm離れた2つの平面の間にあればOKということです。
平行度の測定方法
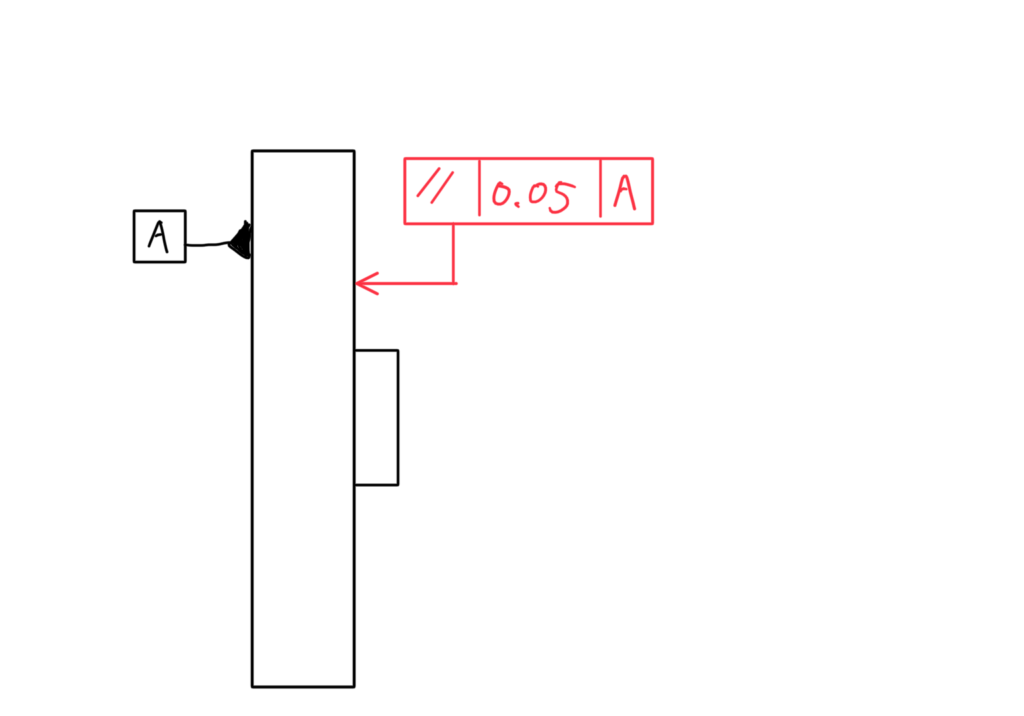
厳密には測定しきれませんが、いつも旋盤で使っている簡易的な測定方法を書いておきます。
丸ものでは、上図のように端面同士に平面度公差が入っていることが多いです。
その場合、マイクロメーターで一番外側の寸法を何箇所か測り、その差が0.05mm以下であれば平行度が0.05以下であると判断しても差し支えありません。
板ものでも同様に平行度を簡易的に測定できますので、試してみてください。
直角度
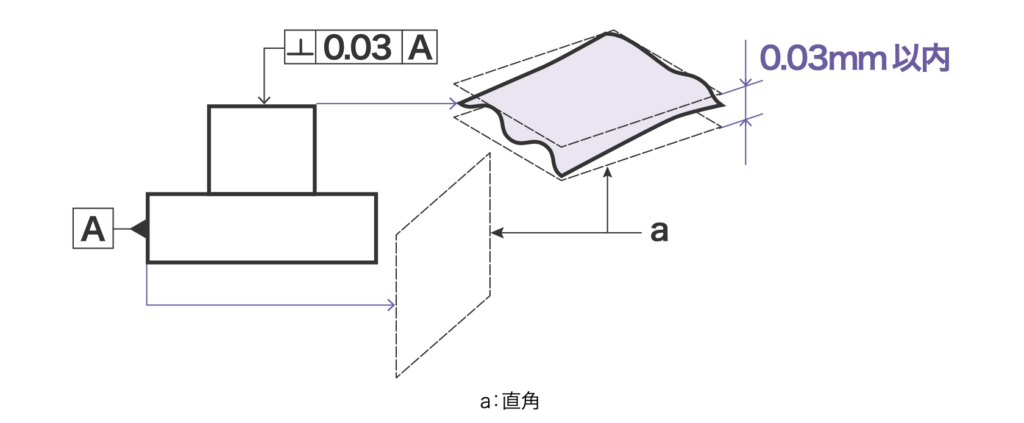
データム直線またはデータム平面に対して直角な幾何学的直線または幾何学的平面からの直角であるべき直線形体または平面形体の狂いの大きさ
機械製図 実教出版
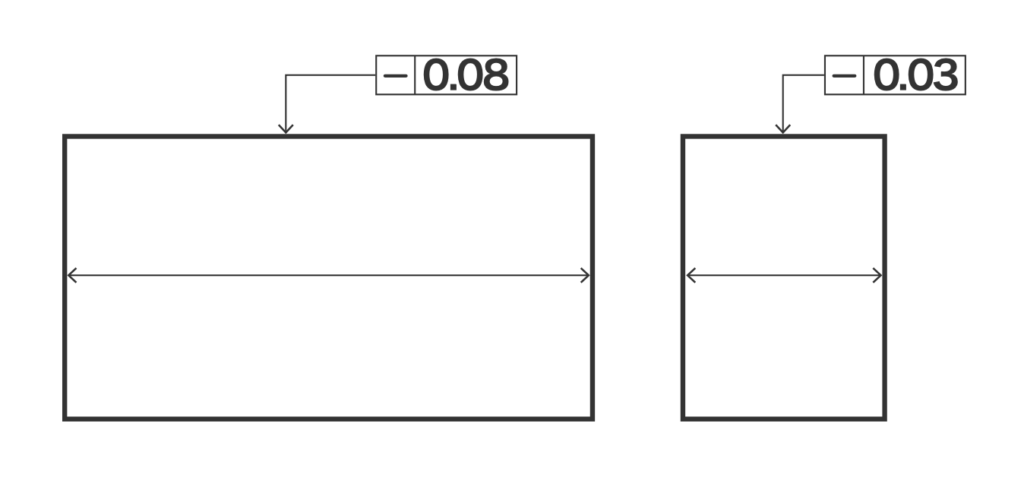
図は少しわかりにくいですが、要するにデータムに対してどのくらい直角であるかを指定した公差です。
上図の場合0.03mmの直角度が指定されているため、データムAの平面に対して直角な面から0.03mm以内のズレであればOKといった具合です。
旋盤加工品で直角度が入っている場合、直角度が入っている箇所とデータムが1回のクランプで加工できるものであればほぼ確実に直角度は出るので全く難しくありません。
ですが1工程目に加工する箇所と2工程目に加工する箇所間をまたがって直角度が指定されている場合はしっかり芯出しをしておかないと直角度を外す可能性が出てきます。
直角度の測定方法
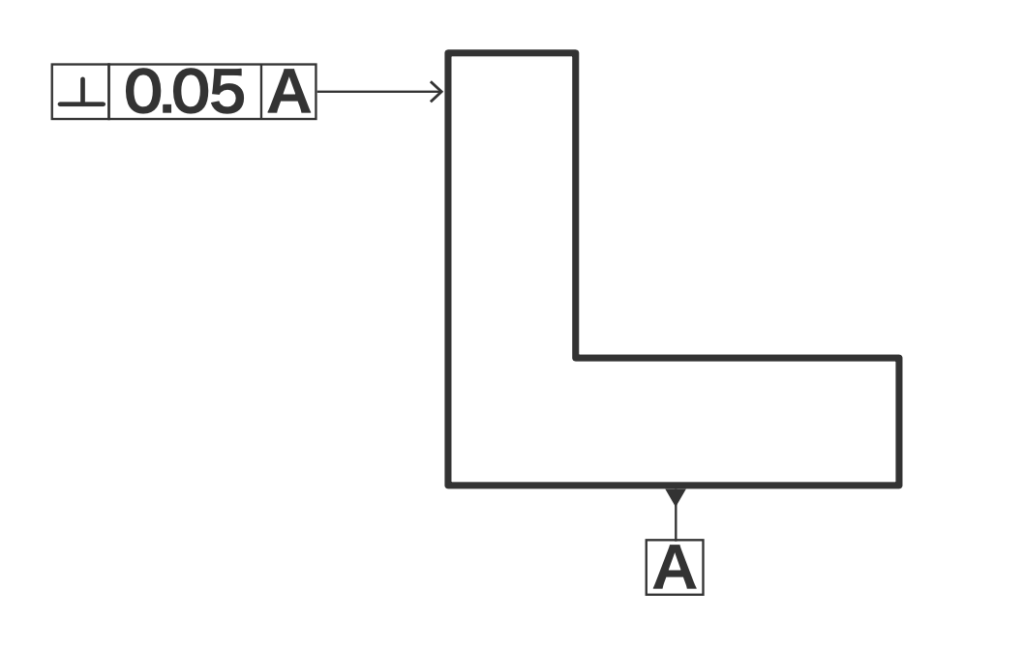
丸ものの場合は、旋盤で掴んで芯を出した上で刃物台に取り付けたてこ式ダイヤルゲージを上下に走らせ、直角がどのくらい出ているかを確認します。
上画像のような板ものの場合も同様で、フライス盤・マシニングセンタのバイスでワークをまっすぐに掴み、主軸付近に取り付けたダイヤルゲージを上下に走らせて直角度を測定します。
傾斜度

データム直線またはデータム平面に対して理論的に正確な角度を持つ幾何学的直線または幾何学的平面からの理論的に正確な角度を持つべき直線形体または平面形体の狂いの大きさ
機械製図 実教出版
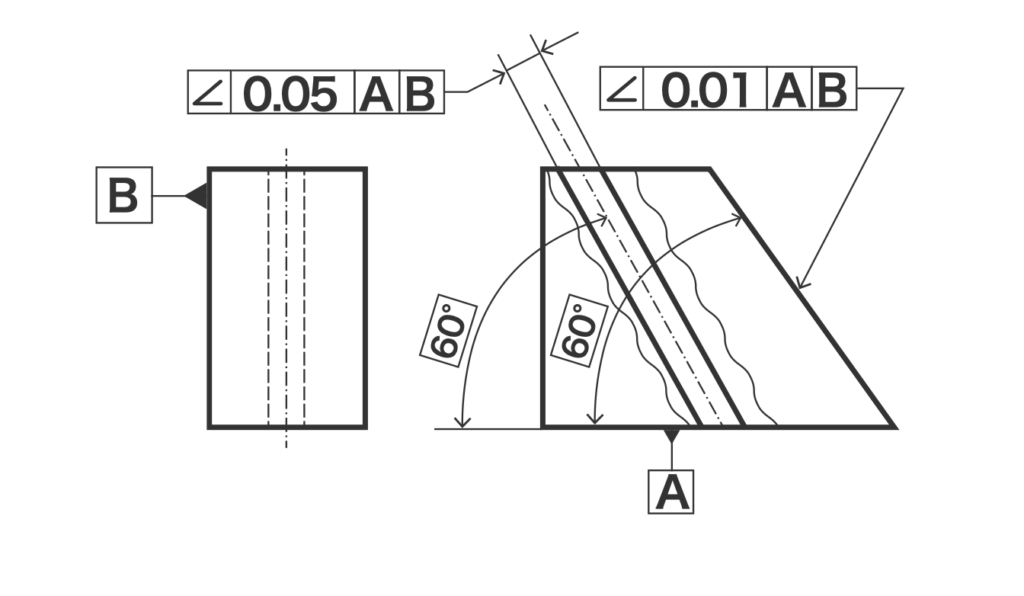
傾斜度は、データムで指示された面に対して正確に傾いているかということを示した幾何公差です。
ここで大事になってくるのは、傾斜度が指示しているのは図のように角度ではなく長さということです。
上図の例であれば指示された平面が、理想的な面を中心にして0.3mm離れた平面同士の間になければならないということで、角度の誤差が0.3°以内ということではありません。
傾斜度の測定方法
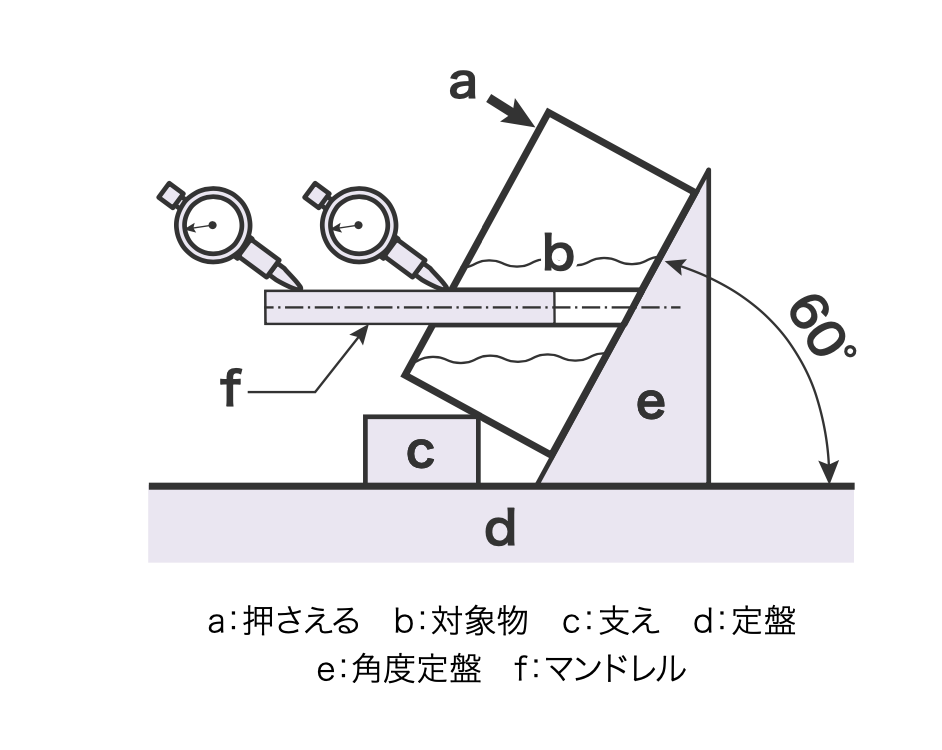
傾斜度を0.01mm台まで本当に正確に測定しようと思うとそこそこ大変な準備が必要になります。
まずは角度定盤が必要です。
正確な角度にワークを傾けた上で、測定箇所が図のように平行になっていることをダイヤルゲージを使って確認します。
そもそも職場に角度定盤はありませんし、ここまで正確に傾斜度を測る必要が生じたこともありません。
道具が揃っていない場合はあまり現実的な測り方ではありませんね。
なので現場で角度を正確に測る必要が生じたときはキーエンスの簡易三次元測定機を使っています。
位置度
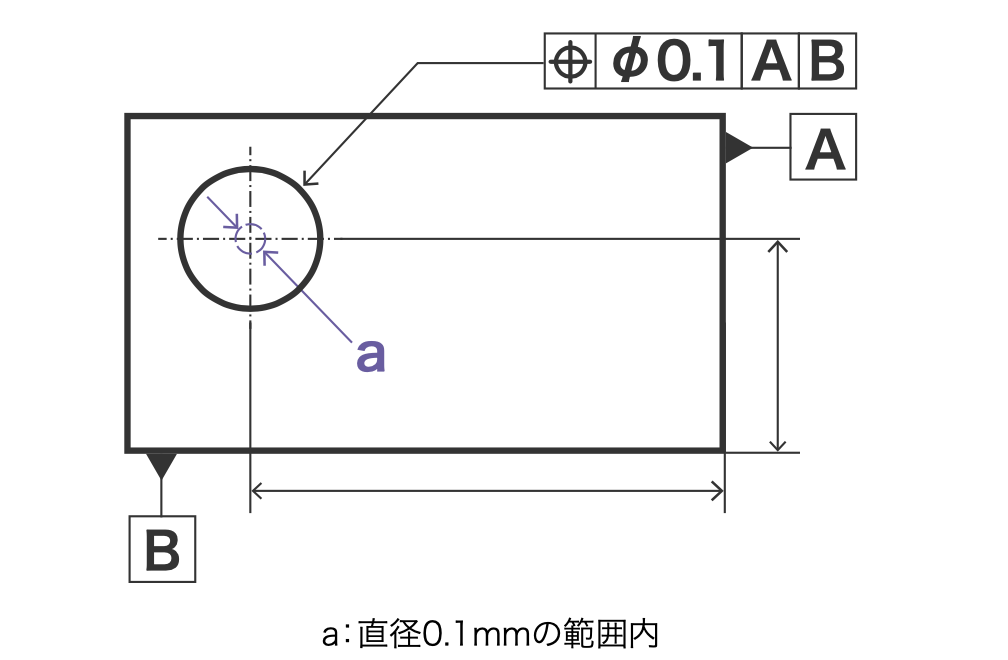
データムまたはほかの形体に関連して定められた理論的に正確な位置からの点、直線形体、または平面形体の狂いの大きさ
機械製図 実教出版
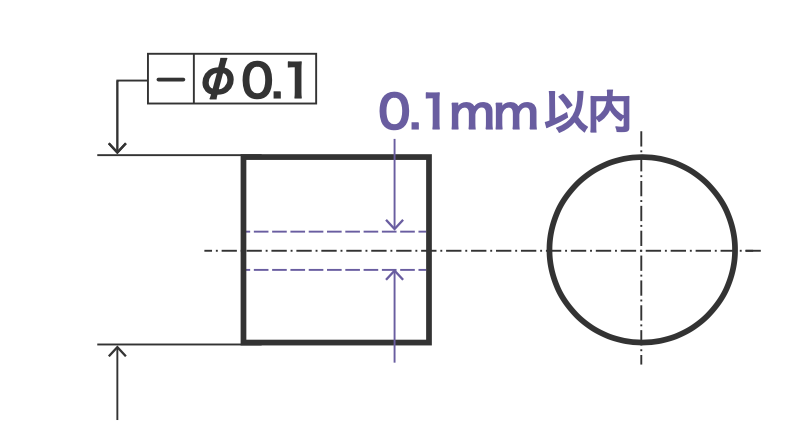
位置度は、穴などがどのくらい正確な位置にあるかを示した公差です。
旋盤加工だと全く見たことがない幾何公差で、主にリーマ穴あけなどフライス加工で使われる公差です。
画像の例だと、指定された寸法の中心点から直径0.1mmの範囲内に穴中心が来ていればOKです。
寸法公差の+-0.1との違いは、寸法公差だと許容範囲が四角形になるのに対し、位置度公差だと許容範囲が円形になるということです。
細かな違いはあれど、一番寸法公差に近い幾何公差なので理解はしやすいかと思います!
位置度の測定方法
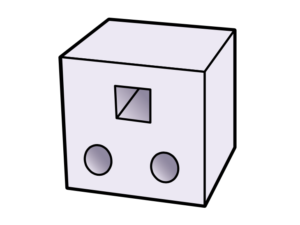
位置度の測定は、厳密には画像のような検査ゲージを作って測るのが間違いありませんが、現場ではいちいちそんなゲージを作っていられませんよね。
先述のように位置度は寸法公差に最も近い公差なので、通常の寸法公差と同じように穴位置等を測定し、その寸法が位置度の許容差内かどうか確認する方法が現実的です。
同心度・同軸度・円周振れ・全振れ

次は旋盤加工でしょっちゅう見かける同軸度と同心度です。
この2つの幾何公差、両方とも上記の二重丸のマークを使います。
ですが図面の指示の仕方で2つに分かれる、ある意味特殊な幾何公差です。
一つずつ説明していきますね。
同心度
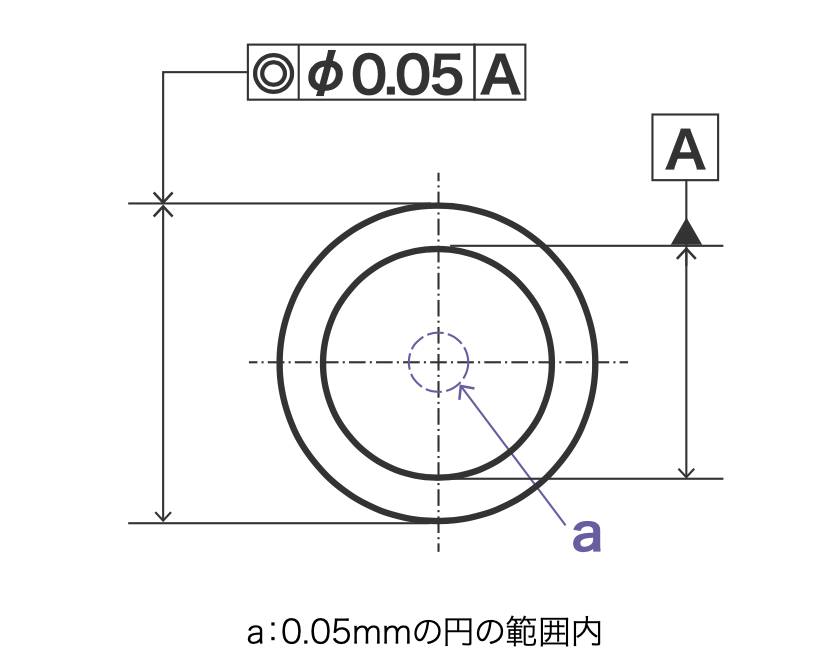
データム円の中心に対するほかの円形形体の中心の位置の狂いの大きさ
機械製図 実教出版
上図のように、丸を端面方向から見た書き方の場合は同心度です。
同心度の意味は上図の例であれば、指示された円の中心点がデータムで示された円の中心点から0.05mm以内の距離でないといけないということ。
つまり、中心点がズレていないことを示す公差です。
この中心点というところがミソで、同軸度は中心線になります。
同軸度
データム軸直線と同一直線上にあるべき軸線のデータム軸直線からの狂いの大きさ
機械製図 実教出版
上図のように、同じ記号でも外径方向から見た書き方の場合は同軸度になります。
同軸度の意味は、上図の例であれば、指示された円筒の軸線がデータムで示された軸線から0.03mm以内の距離になければならないということです。
つまり、中心軸(中心線)がズレていないことを示す公差です。
このように、図面の書き方で同じ記号でも点と線で意味合いが変わってくるんです。
円周振れ

データム軸直線を軸とする回転体をデータム軸直線のまわりに回転したとき、その表面が指定された位置または任意の点において指定された方向に変異する大きさ
機械製図 実教出版
この幾何公差もたまに見ます。
この幾何公差の内容としては、「回転させたときの円周の一部の振れ」なので、図のように指定された箇所の円周振れが0.03mm以内に収まっていれば良いです。
このように厳密には同軸度や同心度と異なりますが、旋盤加工を行うにおいては測定方法も同じですし、同軸度や同心度と同じものとして捉えても差し支えありません。
全振れ
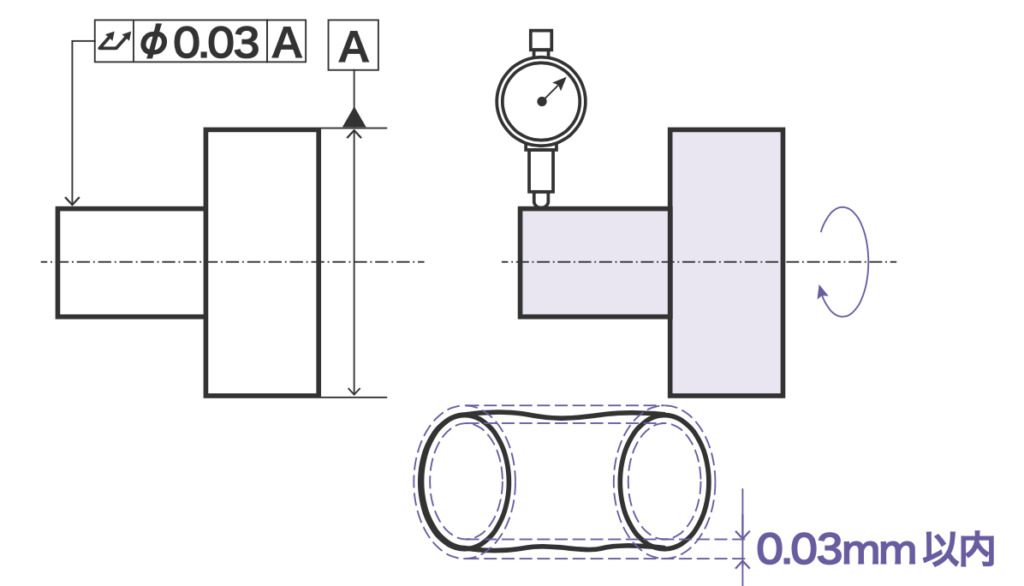
データム軸直線を軸とする回転体をデータム軸直線のまわりに回転したとき、その表面が指定された方向に変異する大きさ
機械製図 実教出版
全振れはあまり見ない幾何公差ですが、同軸度にかなり近い公差です。
円周振れが”指定された一部の振れ”だったのに対して、全振れは「回転させたときの表面全体の振れ」をしています。
図のように、円周全体の測定値の振れが0.03mm以内だとOKで、同軸度との違いは軸か表面かというだけのものです。
厳密には意味は違うがやることは同じ
同心度と同軸度、円周振れ、全振れには上記のように違いがありますが、これら全て偏心させないようにするという意味では同じなので、旋盤加工においては同じように芯を出して加工すればOKです。
三つ爪チャックであれば芯の出た生爪を使い、しっかり芯を出して加工することで同心度・同軸度・円周振れ・全振れ全てに同じように対応することができます。
同心度・同軸度の測定
測定方法も同心度と同軸度、円周振れ、全振れに特に差はありません。
主に測定方法は2つです。
・旋盤で芯出しをしてワークをつかみ、回転させてダイヤルゲージで芯振れを見る方法
・Vブロックなどに置いたワークを回転させて、ダイヤルゲージをあてて芯振れを測定する方法
2つの方法とは言いましたがVブロックか旋盤かという違いだけで、やっていることは同じです。
この4つの幾何公差をまとめて考えられるようになれば、苦手意識を持ちやすい幾何公差の理解がすっきりすると思います!
参考文献
本記事はキーエンスHP https://www.keyence.co.jp より画像を一部引用させていただいています。









コメント